Project C-T1 - Sensor Fusion in Cortical Circuits: Modeling and Behavioral Experiments in Man and Machine

The approach to instantiating computation and engineering novel computational algorithms has been highly successful, especially for solving problems that can be formalized as a mathematical relation from input to output. However, the problem of extracting more reliable data from ambiguous and noisy real-world environment is still more resistant to straightforward solutions, often requiring elaborate theoretical reasoning and significant processing resources. 

The main computations performed by brain involve nonlinear transformations (e.g. sensory- motor transformations), cue integration, or both [1]. For instance, to reach an object by hand, one must configure the arm joints with respect to the visual location of the object and proprioceptive cues (e.g. position of body or eyes). Accessible sensory information is often uncertain and ambiguous, but humans can perceive and estimate the state of the real world, and consequently handle cognitive tasks efficiently despite the presence of noisy signals. Sensory perception in cortical areas is provided by multiple paths of information targeting uni-modal or multi-modal areas of the brain, which often mutually effect each other. Some simulations of cortically inspired computational frameworks with hand-crafted connectivity have shown how de-noising, inference and sensor perception can possibly be handled by the brain [2]. Recently an unsupervised framework of relation learning between two interacting populations of neurons has been proposed, which allows the network to learn arbitrary relations between two sensory variables [3]. However, a flexible computational framework which could learn relationships between cues rather than using fixed networks still needs to get addressed as a challenge, especially in the presence of higher order modalities [3]. 

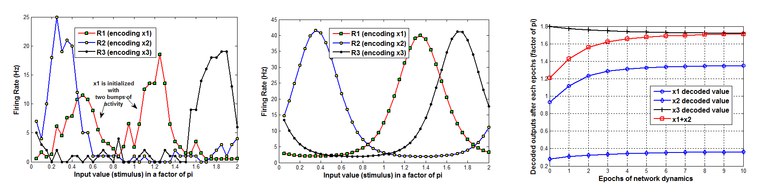
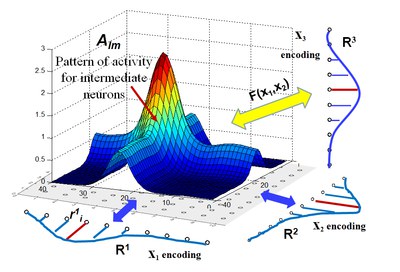
We have suggested a flexible multiple cues integration framework by which the network is capable of learning arbitrary relations between one of the encoded sensory variables as a function of other variables using biologically realistic algorithms like Hebbian learning, Divisive Normalization, and winner-takes-all [4]. The network thereby provides scalable computational machinery for relation satisfaction using attraction dynamics. We demonstrate that after constructing plastic synaptic weights, the network can perform several principle computational tasks such as inference and reasoning, de-noising, cue-integration and decision making. Two important features of this framework are its scalability to cases with higher order of modalities and its flexibility to realize smooth functions of relations.